Atonal Assistant is designed to aid in the analysis and composition of atonal music. Because it runs in a Web browser, it is very convenient to use and the data it generates may easily be transferred to homework assignments, term papers, and scholarly articles. Atonal Assistant is designed for students rather than experts. It allows students to check their theoretical calculations and freely explore the pitch-class set universe. It also offers a number of strictly pedagogical modules including the Mod 12 Calculator and Interval Calculator.

Enter a pc set and Atonal Assistant will report its normal form, prime form, and ic vector, as well as other important information. So that sets may be easily recalled, the program keeps a running tab of the sets that are examined in its History Area. It can also: display a set using staff notation; list a set's interval succession; identify basic relations (complement, Z and M) and aspects of symmetry; produce common-tone structure vector, scoreboards, and index matrices; and perform the operations transposition (T_n), inversion (T_nI), and M-operation (M_n).

A working knowledge of atonal theory is required to use Atonal Assistant. Kostka and Payne (2008) is recommended for those requiring a brief introduction to the subject. Those who require a more thorough introduction should consult Straus (2005) or Rahn (1980). Atonal Assistant's features are compatible with the terms, definitions and symbols found in Straus (2005) and Kostka and Payne (2008), as well as a variety of other texts. See section 9. Feature Definitions for more information.

Atonal Assistant is in the final stages of its development. Your comments and suggestions are welcome. Please send them to rbain@mozart.sc.edu.

2. Getting Started

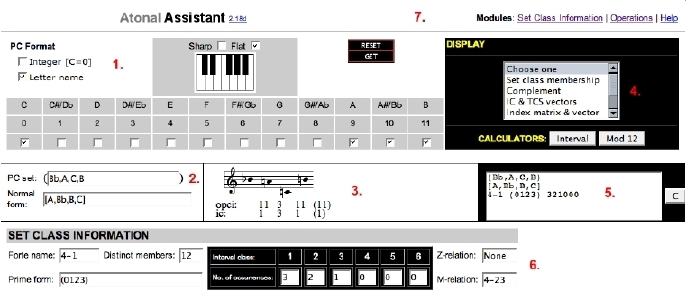
Atonal Assistant's top-level interface is shown in Fig. 1.

Fig. 1. Twelve-Tone Assistant's top-level interface.

The set in the Set Notation Area's PC set field is called the current pc set. In Fig. 1 the current pc set is:

(Bb,A,C,B)

the so-called Bach motive. We will use this set for all of the figures and examples. So you can quickly get started using Atonal Assistant, the seven interface areas numbered in Fig. 1 are briefly introduced below.

1. The PC Entry Area

The Pitch-Class (PC) Entry Area provides a 1-octave piano keyboard and twelve HTML checkboxes that allow you to enter a pc set. The PC Format checkboxes control how the set is notated. You can choose between two pc formats: (1) Integer [C=0], and (2) Letter name (see section 4.2). To start the entry process over, click the Reset button (see section 3.5). This will clear the current set and associated data fields. Click the Get button to report the normal form (see section 3.6), staff notation (see section 4.4), and set class information (see section 5.2) for the current set. See section 3. Entering PC Sets for more information.

2. The Set Notation Area

The Set Notation Area has two fields: (1) PC set, and (2) Normal form. The PC set field lists the current set using the current pc format. You can also enter a set by typing its pitch classes directly into this field (see section 3.3), or by copying a previously entered set from the History Area (see section 8). To calculate the Normal form of the current set, click the Get button (see section 3.6).

3. The Staff Notation Area

Clicking the Get button also displays the staff notation for the current set. The set's interval succession is listed below the staff. See section 4.3 Staff Notation for more information.

4. The Display Menu and Calculators Area

The Display Menu provides access to more information about the set, as well as its relation to other sets. Atonal Assistant can display the current set's: set class membership, literal and abstract complement, TCS vector, index matrix, and index vector (also called TICS vector). This area also offers a number of strictly pedagogical features including the Interval Calculator and Mod 12 Calculator. See section 6. The Display Menu and 7. Calculators for more information.

5. The History Area

Every time you click the Get button the current set, along with its normal form, set class information and ic vector, are listed in the History Area using Straus notation (see section 4.5). The History Area is designed to provide an easy way to recall a previously entered set. See section 8. The History Area for more information.

6. The Modules Area

Atonal Assistant's Set Class Information (see section 5.2) and Operation (see section 5.4) modules load into the Modules Area frame located at the bottom of the program. Use the links provided in the Title Area (see below) to load these modules. When Atonal Assistant is launched, the Set Class Information module is automatically loaded. See section 5. Module Selection for more information.

7. The Title Area

Atonal Assistant's logo, version number, and access to the Set Class Information, Operations, Help, and Self-Tests modules are provided in the Title Area. Click the version number to show the latest software distribution's release notes. Click the Help link to load the Help module (this document) which loads in a new HTML window. Atonal Assistant's Self-Tests module offers the opportunity for unlimited drill on selected concepts. See section 9. Self-Tests Menu for more information.

Atonal Assistant provides three ways to enter a pc set:

1. Click on the keys of the PC Entry Area's 1-octave piano keyboard (see section 3.1).
2. Click on the PC Entry Area's pc checkboxes (see section 3.2).
3. Type pitch classes directly into the Set Notation Area's PC Set field (see section 3.3).

Each method is discussed below.

3.1 The 1-Octave Keyboard

Fig. 2 shows Atonal Assistant's PC Entry Area.

Fig. 2. The PC Entry Area.

As you enter pitch classes, they appear one at a time in the Set Notation Area's PC Set field (See Fig. 3). The order in which you enter the pitch classes is retained and the pc checkboxes are checked to match your entry.

Fig. 3. The Set Notation Area.

When the pc format is Letter name, you may note an enharmonic preference using the Sharp and Flat checkboxes above the 1-octave keyboard for C# /Db, D# /Eb, F# /Gb, G#/Ab, and A#/Bb. See section 4.3 Enharmonic Preference for more information. To remove a pc that has already been entered, click on the corresponding piano key. See section 3.4 Removing a PC for more information.

3.2 The PC Checkboxes

You may also enter a pc set by clicking on the pc checkboxes beneath the 1-octave keyboard (see Fig. 2). Each checkbox represents a fixed-zero pc integer, that is: C=0, C#/Db=1, D=2, D#/Eb=3, E=4, ..., B=11. To remove a pc that has already been entered, click on the corresponding pc checkbox. See section 3.4 Removing a PC for more information. Note that, at any given time, the unchecked checkboxes represent the literal complement (see section 6.12) of the current set.

3.3 Typing Directly into the PC Set Field

You may also enter a set by typing it into the Set Notation Area's PC Set field. When you bring the field into focus, the Normal form field and all set class information fields are cleared. When you exit the field (see section 3.31) using the tab key, Atonal Assistant updates the pc checkboxes to match your entry. The format of your typed entry must match the current pc format (see section 3.32).

3.31 Exiting the PC Set Field

To exit the PC set field, press the tab key, or click anywhere in the program outside the field.

3.32 Entry Format

Your entry's pc format must agree with the current PC Format setting and set members must be separated by commas. Note, however, that intervening spaces between members are ignored. For example, when entering the pc set (D,E,F#):

2,4,6 and 2, 4, 6

are both Integer [C=0] entries. Also keep in mind that enharmonically equivalent Letter name entries, such as:

D,E,Gb and D,Fb,F#

are also valid entries.

3.33 Invalid Entries

If you enter an invalid pc set (see also section 3.6), Atonal Assistant will attempt to parse your entry as best it can, retaining valid pitch classes and discarding invalid ones. To start the entry process over, click the Reset button (see section 3.5). Atonal Assistant will clear the current set and all associated data fields.

3.34 Replacing a PC

You can replace a pc in the current pc set by selecting it and typing over it. The change will take effect when you exit the PC Set field using the tab key (see section 3.31).

3.35 Copying a PC Set from the History Area

You may copy a previously entered set from the History Area.
See section 8. The History Area for more information.

3.4 Removing a PC

To remove a pc that has already been entered, click on the corresponding piano key or pc checkbox.

3.5 The Reset Button

The Reset button clears the current set and all associated data fields so that you may start the entry process over. All pc checkboxes are unchecked and the Set Notation Area's PC set and Normal form fields are cleared. If the Set Class Information Module is loaded, all of its fields are cleared (see section 5.2); if the Operations Module is loaded, its four resultant fields are cleared (see section 5.4).

3.6 The Get Button

Click the PC Entry Area's Get button to display the normal form, staff notation, and set class information for the current pc set. See section 5.2 Set Class Information for more information. If you click the Get button before you have entered a pc set, you will receive the following error message:

4. Set Notation

4.1 PC Symbols

Atonal Assistant uses the following 12 integer and 21 letter name symbols for input and output:

Fig. 4. PC symbols.

PC Integers [C=0]

0

1

2

3

4

5

6

7

8

9

10

11

PC Letter Names (Sharp)

B#

C#

D#

E#

F#

G#

A#

PC Letter Names (Natural)

C

D

E

F

G

A

B

PC Letter Names (Flat)

Db

Eb

Fb

Gb

Ab

Bb

Cb

Each column in Fig. 4 represents one of the twelve pitch classes. The sharp symbol is the '#' symbol (shift-3). The flat symbol is the 'b' symbol (lowercase b). Double-sharps and double-flats are not currently recognized.

4.2 PC Format

Atonal Assistant can convert between the following two pc formats: (1) fixed-zero pc integer, that is:

C=0, C#/Db=1, D=2, D#/Eb=3, E=4, F=5, F#/Gb=6, G=7, G#/Ab=8, A=9, A#/Bb=10, B=11

and (2) pc letter name notation. The PC Format option shown in Fig. 5 affects both pc display and entry. See section 3. Entering PC Sets for more information.

Fig. 5. The PC Format and Enharmonic Preference checkboxes.

When the PC Format is changed, the Set Notation Area's PC set and Normal form fields are immediately updated to the new format. If the Operations module is loaded, all four resultant fields are also updated to the new format (see section 5.4).

4.3 Enharmonic Preference

When the PC Entry Area's PC Format option is set to Letter name, the Sharp and Flat checkboxes above the 1-octave keyboard (see Fig. 5) allow you to record an enharmonic preference for C#/Db, D#/Eb, F#/Gb, G#/Ab, and A#/Bb. Enharmonic preferences will be reflected in all instances of that pitch class when Letter name format is checked. Please note that you can only record an enharmonic preference when the pc format is Letter name.

4.4 Staff Notation

When you click the Get button, the staff notation for the current set is displayed in the Staff Notation Area along with the set's interval succession as shown in Fig. 6.

Fig. 6. The Staff Notation Area.

The interval succession is notated using ordered pitch-class intervals (opci) and interval classes (ic). The "wrap-around interval," the interval between the last and first members of the set, is enclosed in parentheses.

4.5 Straus Notation

Like Kostka and Payne (2008), Atonal Assistant adopts the notation used in Straus (2005). The following table summarizes some of the notational possibilities using the set (Bb,A,C,B):

Note that that 'T" and 'E' are substituted for 10 and 11, respectively, in all prime forms.

Atonal Assistant has three modules:

1. Set Class Information
2. Operations
3. Help (this document)

The Set Class Information and Operation modules load into the Modules Area frame at the bottom of the program. Each module is discussed below.

5.1 Loading a Module

To load a module, click one of the three Modules links in the Title Area shown in Fig. 8.

Fig. 8. The Title Area's modules links.

The Set Class Information module is automatically loaded when the program is launched.

5.2 The Set Class Information Module

Fig. 9 shows the Set Class Information Module.

Fig. 9. The Set Class Information Module.

The set class information for the set is retrieved using the PC Entry Area's Get button. When you click the Get button, Atonal Assistant calculates the prime form of the current set and uses it to look up the following information in its Set Class Database: the Forte name, the number of Distinct members in the set class, the ic vector, the Z-relation (if any), and M-relation (see section 5.21). This information is reported in Fig. 9 for the pc set (Bb,A,C,B). All of the fields in the Set Class Information Module, except for the Forte Name field (see section 5.3), are read-only fields. The ic vector is reported here using scoreboard format. The Straus notation (see section 4.5) for the ic vector (i.e., 321000) is displayed in the History Area, and is also available in the Display Menu's IC & TCS Vector option.

5.21 Z-relation

The Z-relation field displays the Forte name of the set class, if any, that has the same ic vector as the current set class. For example, 4-Z15 (0146) and 4-Z29 (0137) both have the ic vector 111111. If no Z-related set class exists, Atonal Assistant reports "None".

5.22 M-relation

The M-relation field displays the Forte name of the set class that is related to the current pc set by M₇, for example:

M₇ (Bb,A,C,B) = M₇ (10,9,0,11) = mod 12 (7*10, 7*9, 7*0, 7*11) = (10,3,0,5)

The pc set (10,3,0,5) belongs to set class 4-23 (0257), so 4-23 is displayed in the M-relation field. See section 5.41 M-Operations for more information.

5.3 Forte Name Lookup

If you type a valid Forte name symbol into the Forte name field (see Fig. 9), Atonal Assistant will retrieve its associated set class information. When you bring the field into focus, all set class information fields are cleared. Use the tab key, or click anywhere in the program outside of the field, to exit the field and retrieve the information.

5.4 The Operations Module

Shown in Fig. 10, the Operations Module may be used to perform the operations T_n, T_nI, and M_n on the current set.

Fig. 10. The Operations Module.

The operations T₀, T₀I, M₅ and M₇ are entered by default. You may change the value of the index n (0-11) for any one, or more, of the four operations. When you bring an index field into focus, the corresponding resultant set field is cleared. To facilitate comparison between M-operations, two M_n operations may be performed at the same time. Clicking the Calculate button to performs all four operations. The sets that result from these four operations are displayed in the four resultant set fields. All four operations are expressed in algebraic notation, that is:

T_n (X) = Y

where X is current set, and Y is the resultant set after the operation T_n. Resultant sets are displayed using the current pc format. When you change the pc format, the resultant set fields are immediately updated to the new format. In Fig. 10, the current pc set X = (Bb,A,C,B) and the pc format is Letter name.

5.41 M-operations

M_n is the multiplicative operation. The M_n operation multiplies each member of the pc set in turn by the index n. The results are returned Mod 12 as shown in the example below:

M₅ (10,9,0,11) = Mod 12 (5*10, 5*9, 5*0,5*11) = (2,9,0,7)

M₇ (10,9,0,11) = Mod 12 (7*10, 7*9, 7*0,7*11) = (10,3,0,5)

Fig. 11 shows the Display Menu and Calculators Area.

Fig. 11. The Display Menu and Calculators Area.

The Display Menu provides access to more information about the set, as well as its relation to other sets. Each menu item launches a new window containing highly-formatted symbol data that may be transferred (via traditional copy and paste techniques) to a word processor or HTML editor (e.g., using Netscape's Save Page As... or View > Page Source features). The six Display Menu options are: 1. Set class membership, 2. Complement, 3. IC & TCS vectors, 4. Index matrix & vector, 5. Normal form algorithm, and 6. Prime form algorithm. Each option is described below, along with sample output for the set (Bb,A,C,B).

6.1 Set Class Membership

The Set Class Membership window displays the 24 sets related to the current set by T_n or T_nI. Sets are notated in normal form using the current PC Format. The family of 24 sets related to (Bb,A,C,B) by T_nor T_nI, set class 4-1 (0123), is shown below using letter name notation:

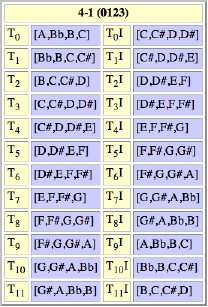
For symmetrical sets, sets that map onto themselves under T_n or T_nI, there will be fewer than 24 distinct members in the set class. The number of distinct members of the set class is reported in the Distinct members field of the Set Class Information module (see section 5.2). Notice that the pc set (Bb,A,C,B) is symmetrical under T_nI, that is:T₉I (Bb,A,C,B) = T₀ (Bb,A,C,B); T₁₀I (Bb,A,C,B) = T₁ (Bb,A,C,B); and so on. Consequently, set class 4-1 (0123) has 12 distinct members rather than 24.

6.2 Complement

The complement (also called literal complement) of a set is the set of all pitch classes that are not members of the current set. For example, using letter name notation:

Atonal Assistant also reports the abstract complement of the current set, that is, the set class to which the complementary set (C#,D,D#,E,F,F#,G,G#) belongs as shown below:

The ic vectors of the current pc set and literal complement are also reported so that the student can discover the relationship that exists between them.

6.3 IC & TCS Vectors

The IC & TCS Vectors option displays the ic vector for the current pc set using Straus notation (see section 4.5) and Rahn (1980) notation as shown below:

It also displays the TCS Vector. TCS stands for transposition common-tone structure. The TCS vector, which is directly related to the ic vector, reports the number of common tones produced under T_n. Proceeding in left-to-right order, the TCS vector reports the number of common tones produced at T₀, T₁, T₂, ..., T₁₁, respectively.

The scoreboard below provides an easy-to-read summary of the information contained in the TCS vector:

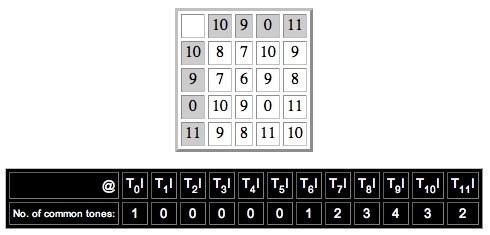
6.4 Index Matrix and Vector

The index vector (Straus 2005), also called the TICS vector (Rahn 1980), reports the number of common tones produced under T_nI. Proceeding in left-to-right order, the vector entries report the number of common tones produced at T₀I, T₁I, T₂I, ..., T₁₁I, respectively, as shown below:

Proceeding in left-to-right order, the TCS vector reports the number of common tones produced at T₀I, T₁I, T₂I ..., T₁₁I, respectively, as illustrated below:

T₀I (Bb,A,C,B) = (D,Eb,C,C#) ; 1 common tone
T₁I (Bb,A,C,B) = (Eb,E,C#,D); 0 common tones
etc.

The index vector is determined by making an index matrix (Straus 2005, pp. 83-85). The index matrix is always given using fixed-zero integer notation. For the pc set (Bb,A,C,B), Atonal Assistant reports that the index matrix and scoreboard are, respectively:

6.5 Normal Form Algorithm

The Normal form algorithm feature is designed to show each step in the Rahn (1980) normal form algorithm for the current set. This strictly pedagogical feature was added at the request of students who wanted to be able to see where their calculations had gone awry.

6.6 Prime Form Algorithm

The Prime form algorithm feature is designed to show each step in the prime form algorithm for the current set. Again, this strictly pedagogical feature was added at the request of students who wanted to be able to see where their calculations had gone awry.

7. Calculators

Atonal Assistant's two pedagogical calculators are introduced below.

7.1 Interval Calculator

Shown in Fig. 12, the Interval Calculator reports the 1. ordered pitch interval, 2. unordered pitch interval, 3. ordered pitch-class interval, 4. interval class (also called unordered pitch-class interval), and 5. traditional tonal interval for any two pitches between C1 and B6 inclusive.

Use the 6-octave piano keyboard to enter Pitch 1 and Pitch 2. Note that middle C, or C4, is the fourth C key from the left. When you position the cursor over a key in the Netscape browser, the pitch, MIDI pitch number, and fixed-zero pitch-class integer appear in the Assistance Area as shown in Fig. 12. Click on the 6-octave keyboard to enter Pitch 1 and Atonal Assistant will automatically advance to the Pitch 2 field, and vice versa. Click the Interval Calculator's Calculate button to calculate the five associated interval types. Click the Reset button to clear all fields and start the entry process over.

7.12 Traditional Tonal Interval

Traditional tonal interval names are reported as simple intervals, that is, up or down, within the octave inclusive.

7.2 Mod 12 Calculator

The Mod 12 Calculator shown in Fig. 13 resembles a traditional calculator, however, it performs Modulo 12 (abbreviated Mod 12) addition, subtraction and multiplication.

Fig. 13. The Mod 12 Calculator.

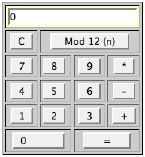The Mod 12 (n) button can be used to return the Mod 12 equivalent of any integer. To enter a negative number, click the minus key '-' before you enter a number. A few sample calculations should serve to demonstrate the calculator's basic functions, as well as its usefulness for pitch-class interval calculations.

10 + 2 = 0
2 + 2 = 4
11 + 4 = 3
4 - 6 = 10
-3 + 2 = 11
5 - 10 = 7
3 * 4 = 0

Please note that all operations are performed on the two previous entries, that is, you cannot perform operations like 3 + 3 + 3 = 9 which require more than two operands.

8. The History Area

Every time you click the PC Entry Area's Get button, the History Area lists the current set, its normal form, set class membership, and ic vector as shown in Fig. 14.

Fig. 14. The History Area.

The listing is presented on 3 lines using Straus notation (see section 4.5) and the current pc format as follows:

1. The current set

2. The normal form of the current set

3. The current set's set class information: Forte name, prime form, and ic vector (separated by a space).

8.1 Copying a Set to the PC Set Field

You can select any set in the History Area and copy and paste it into the Set Notation Area's PC set field. This provides a convenient way to recall a previously entered set. Be sure not to include the parentheses or square brackets in your selection.You can clear the History Area at anytime by clicking the C button.

9. The Self-Tests Module

Atonal Assistant's Self-Tests Module offers the opportunity for unlimited drill on selected concepts including: normal form, prime form, T_n, and T_nI. Shown in Fig. 15, the Self-Tests Menu is located in Atonal Assistant's Title Area.

Fig. 15. The Self-Tests Menu.

Select a self-test from the menu and click the GO button to load it into the Modules Area. The pc format of your answers must match the current pc format settings in the PC Entry area. Pitch classes must be separated by commas and should not include include extra spaces. When you select Integer or Letter Name format in the PC Entry Area, Atonal Assistant will generate a brand new set using that format. When the Sharp option is chosen all-sharps notation is used; when the Flat option is chosen all-flats notation is used. Each self-test is described below.

9.1 The Normal Form Self-Test

When the Normal Form Self-Test Window loads, Atonal Assistant generates a random set of cardinality 3 and enters it into the PC set field as shown in Fig. 16.

Fig. 16.The Normal Form Self-Test window.

Calculate the normal form of the given set and enter it into the blank field provided. The format of your answer must match the current PC Format. Click the Check button to check your answer, if your answer is incorrect you will be asked to try again. Click the Get button at any time to see the correct answer. Click the Go On button to generate a new pc set. Use the Cardinality menu to choose the number of members (3-9) in the new set. Use the Transfer button to transfer the set to the Set Notation Area's PC set field and display its staff notation in the Staff Notation Area (see section 9.21).

9.2 The Prime Form Self-Test

When the Prime Form Self-Test Window loads, Atonal Assistant generates a random set of cardinality 3 and enters it into the PC set field as shown in Fig. 17.

Fig. 17.The Prime Form Self-Test window.

Enter the prime form in the blank field. Click the Check button to check your answer. If your answer is incorrect, you will be asked to try again. Click the Get button at any time to see the correct answer. Click the Go On button to generate a new pc set. Use the Cardinality menu to choose the number of members (3-9) in the new set. Use the Transfer button to transfer the set to the Set Notation Area's PC set field and display its staff notation in the Staff Notation Area (see section 9.21).

9.21 The Transfer Button

It's easier to determine the prime form of a set if you can see its normal form. Click the Transfer button to transfer the set to the Set Notation Area's PC set field and display its staff notation as shown in Fig. 18. Click the PC Entry Area's Get button to display the normal form of the set.

Fig. 18. Using the Transfer function button.

When the set is transfered to the Set Notation Area's PC set field, it becomes Atonal Assistant's current set.

9.3 The Tn Self-Test

When the Tn Self-Test Window loads, Atonal Assistant generates a random set of cardinality 3 and enters it into the PC set field as shown in Fig. 19.

Fig. 19.The Tn Self-Test Window.

Apply the Tn operation to the randomly-generated set and enter the "=" field. For example, in Fig. 19,

T₆ (7,5,11) = (1,11,5)

Click the Check button to check your answer. If your answer is incorrect, you will be asked to try again. Click the Get button at any time to see the correct answer. Click the Go On button to generate a new pc set. Use the Cardinality menu to choose the number of members (3-9) in the new set. Use the Transfer button to transfer the set to the Set Notation Area's PC set field and display its staff notation in the Staff Notation Area (see section 9.21).

9.4 The TnI Self-Test

When the TnI Self-Test Window loads, Atonal Assistant generates a random set of cardinality 3 and enters it into the PC set field as shown in Fig. 20.

Fig. 20.The TnI Self-Test Window.

Apply the TnI operation to the randomly-generated set and enter the "=" field. For example, in Fig. 20,

T₁₁I (7,5,11) = (4,6,0)

Click the Check button to check your answer. If your answer is incorrect, you will be asked to try again. Click the Get button at any time to see the correct answer. Click the Go On button to generate a new pc set. Use the Cardinality menu to choose the number of members (3-9) in the new set. Use the Transfer button to transfer the set to the Set Notation Area's PC set field and display its staff notation in the Staff Notation Area (see section 9.21).

10. Feature Definitions

A working knowledge of basic atonal theory is required to use Atonal Assistant. The program's features are consistent with the terms, definitions and symbols employed in Kostka and Payne (2008), which adopts the notation found in Straus (2005). Precise definitions of the following terms (listed in alphabetical order) may be found in Straus (2005) on the following pages:

Complement, pp. 93-96
Distinct members, p. 91
Forte name, pp. 58-59
IC vector, pp. 14-15
Index matrix, pp. 83-85
Index vector, pp. 83-85 and 265-67
Intervals, pp. 6-13
Mod 12, pp. 5-6
Normal form, pp. 35-36
PC set, pp. 33-34
Prime form, pp. 57-58
Z-relation, pp. 91-93

The term M-relation is borrowed from Castine (1994), pp. 36-39. The term TCS vector was adapted from Rahn's TICS vector.

11. Troubleshooting

1. If you can't see all of Atonal Assistant's interface, resize the browser window as necessary.
2. If Atonal Assistant will not load, check your browser preferences to be sure that JavaScript is enabled.
3. If the Display Menus, Interval Calculator, or Mod 12 Calculator will not load, check your browser preferences to be sure that Block Pop Up Windows is set to off.
4. If Atonal Assistant loads but does not seem to be functioning correctly, click your browser's Reload button while holding down your computer's shift key. This will force the entire program and all of its media assets to reload from the server.
5. If you mistype your User Name or Password and cannot successfully log in to the program, quit your browser, restart it, and try again.

If these steps do not fix the problem, please send an e-mail message to the author at rbain@mozart.sc.edu. Be sure to include information about your computer, operating system, and browser version, along with your description of the problem. Click here to run a script that automatically identifies your browser and operating system. Please copy and paste this information into any e-mail message you send the author.

12. References

Castine, Peter. Set Theory Objects: Abstractions for Computer-Aided Analysis and Composition of Serial and Atonal Music. Berlin: Peter Lang, 1994.

Forte, Allen. The Structure of Atonal Music. New Haven: Yale University Press, 1973.

Kostka, Stefan. Materials and Techniques of Twentieth-Century Music, Third Edition. Upper Saddle River, NJ: Prentice Hall, 2006.

Kostka, Stefan and Dorothy Payne. Tonal Harmony: With An Introduction to Twentieth-Century Music, Sixth Edition. New York: McGraw Hill, 1980.

Rahn, John. Basic Atonal Theory. New York: Longman, 1980.

Straus, Joseph. Introduction to Post-Tonal Theory, Third Edition. Upper Saddle River, NJ: Prentice Hall, 2005.