Mathematical Terms & Concepts

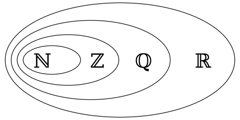Number Sets

1. Natural numbers () {WP}
2. Integers () {WP}
3. Rational numbers () {WP}
4. Real numbers () {WP}
• Irrational numbers {WP}
5. Prime numbers {WP; MW; OEIS}
• Sieve of Eratosthenes {WP}

Number Sequences

1. Natural numbers, also called the positive integers {WP; OEIS}
   1, 2, 3, 4, 5, ...
2. Powers of 2 {WP; OEIS}
   1, 2, 4, 8, 16, 32, 64, ...
3. Primes {WP; OEIS}
   2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...

Arithmetic

1. Arithmetic {MW; WP}
2. Operations
• Addition (+) {MW; WP}
• Subtraction (-) {MW; WP}
• Multiplication (x, or *) {MW; WP}
• Division (÷, or /) {MW; WP}
• Exponentiation (see below)
3. Order of Operations: PEMDAS {WP}
4. Fundamental theorem of arithmetic {MW; WP}

Fractions {Calculator: Wolfram Alpha}

1. Ratio {MW}
   a:b
2. Fraction {WP}
   a/b
• Numerator (a)
• Denominator (b)
3. Superparticular ratio {WP}
   (n+1)/n, where n is a positive integer; e.g., 3/2, 4/3, 5/4, 9/8, 10/9, etc.
4. Simplifying (or reducing) fractions {WP}
   e.g., 4/2 = 2/1; 6/4 = 3/2, 12/6 = 2/1, 80/64 = 5/4, etc.
5. Ratio under octave reduction {XW}
   e.g., 3/1 = 3/2, 4/1 = 2/1, 5/1 = 5/4, 6/1 = 6/4 = 3/2, 7/1 = 7/4, etc.
   
6. Reciprocal {WP}
   The reciprocal of x is 1/x
   
7. Multiplying a fraction by another fraction {WP}
   e.g., 3/2 × 4/3 = 2/1; 9/8 × 9/8 = 81/64; 9/8 × 5/4 = 45/32, etc.
   
8. Dividing a fraction by another fraction
   e.g., 2/1 ÷ 4/3 = 2/1 × 3/4 = 6/4 = 3/2
9. Decimal expansion {MW}
   e.g., 3/2 ≈ 1.5; 4/3 ≈ 1.333, 5/3 ≈ 1.667; etc.
10. Approximation {WP; MW}
11. Rounding {WP; MW}
• e.g., round 701.995 ¢ to the nearest cent ≈ 702 ¢ {Calculator: Wolfram Alpha}
• e.g., round 386.31371 ¢ to 3 decimal places ≈ 386.314 ¢ {Calculator: Wolfram Alpha}
• e.g., round 315.64129 ¢ to 1 decimal place ≈ 315.6 ¢ {Calculator: Wolfram Alpha}
12. Divisor, or factor {WP}
13. Least common multiple (LCM) {WP; Calculator: Wolfram Alpha}
    e.g., LCM (4, 6) = 12; LCM (3, 5) = 15; LCM (4, 5, 6) = 60, etc.
    
14. Lowest common denominator (LCD) {WP; Calculator: Calculator Soup}
    e.g., LCD (1/2, 2/3) = 6; LCD (5/12, 11/18) = 36; LCD (1/2, 1/3, 1/4) = 12; etc.
    

Exponentiation

1. Exponentiation (^) {WP}
   e.g., 2^3 = 2 × 2 × 2 = 8;
   e.g., 12-tet: 2^(1/12) ≈ 1.059; 2^(3/12) ≈ 1.189; 2^(7/12) ≈ 1.498, etc.
2. nth root {WP}
   
   e.g., 12-tet: 2^(1/12) ≈ 1.059; 17-tet: 2^(1/17) ≈ 1.042; 31-tet: 2^(1/31) ≈ 1.023; etc.
3. Calculator: Exponents Problem Solver {Wolfram Alpha}

Logarithm

1. Logarithm (log) {WP}
   e.g., log₁₀(1000) = 3, or 10^3 = 1000; log₂(8) = 3; i.e., 2^3 = 8; log₁₀(3/2) = log₁₀(1.5) ≈ 0.176
2. Cent (c) {WP}
   c = 1200 log₂ (f₁/f₂)
   e.g., 2/1 = 1200¢; 1/1 = 0¢; 2^(1/12) = 100¢; 3/2 ≈ 702¢; 4/3 ≈ 498¢ (rounded to the nearest cent)
   e.g., 81/80 ≈ 21.5¢ (rounded to the nearest 1/10 cent)
   
3. Calculators:
• Bain, Ratio to Cents {ReginaldBain.com}
• Logarithms Solver {Wolfram Alpha}

1. Euclid's Elements (c300 BCE) {WP}
2. Euclidean geometry {WP}
3. Plane {WP}
4. Dimension {WP}
• 1D; 2D 3D; 4D; etc.
5. Line {WP; MW}
6. Pythagorean theorem {WP}
• Square root of 2 {WP}
7. Pythagorean means {MW; WP}
• Arithmetic mean (AM)
• Harmonic mean (HM)
• Geometric mean (GM)
8. Circle {WP; MW}
9. Spiral {WP}
10. Strähle construction {WP; HFF}

Advanced

1. Continued fractions {WP}
2. Coprime integers {WP}
3. Farey sequence {WP; OEIS}
4. Fibonacci sequence {WP; OEIS}
   0, 1, 1, 2, 3, 5, 8, 13, ...
5. Golden ratio {WP}
6. Klein four-group {WP}
7. Pascal's triangle {WP}
8. Prime counting function {WP}
9. Projective plane {WP}
10. Rhombus {WP}
11. Rieman Zeta function {XW}
12. Tessellation, or tiling {WP}
• Triangular tiling {WP}
• Hexagonal tiling {WP}
13. Triangular numbers {WP; OEIS}
    1, 3, 6, 10, 15, 21, ...
14. Topology {WP}
15. Torus {WP}

* * *

Image credits: Click on an image to see the credit

Links

References

Benson, David. 2007. Music: A Mathematical Offering. Cambridge: Cambridge University Press. {GB; Website}

Fauvel, John, Raymond Flood, and Robin Wilson, eds. 2003. Music and Mathematics: From Pythagoras to Fractals. New York: Oxford University Press. {GB}

Gann, Kyle. 2019. The Arithmetic of Listening: Tuning Theory and History for the Impractical Musician. Urbana, IL: University of Illinois Press. {GB; Full text: EBSCOhost; Audio Examples}

Hardy, G. H. and E. M. Wright. 2008/1936. An Introduction to the Theory of Numbers, 6th ed. London: Oxford University Press.

Loy, Gareth. 2006. Musimathics: The Mathematical Foundations of Music, Vol. 1-2. Cambridge, Mass: MIT Press. {Website; Full text: Vol. 1 Musical Elements: Ebook Central; Vol 2 Musical Signals: Ebook Central}

Marecek, Lynn, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis. 2020. Prealgebra, 2nd e. Houston, TX: OpenStax. {OpenStax}

Sloane, N. J. A. 1964. The Online Encyclopedia of Integer Sequences (OEIS). Available online at: <https://oeis.org>.

Weisstein, Eric, ed. 2021. Wolfram MathWorld – A Wolfram Web Resource. Available online at: <https://mathworld.wolfram.com>. 

Updated: April 14, 2024