Scripting Web Apps for Music Theory
using SVG & Web Audio API

Abstract

Scalable Vector Graphics (SVG) and Web Audio API are two powerful web-browser technologies that may be used to create interactive web apps for music theory. This paper discusses a JavaScript web app for geometrical music theory that employs SVG and Web Audio API. The app generates an interactive 12-tone equal tempered pitch-class clockface diagram, a traditional model for pitch-class space in post-tonal theory, that uses SVG to display all possible polygon diagrams and Web Audio API to play a given polygon’s associated chord and rhythmic timeline.

Example

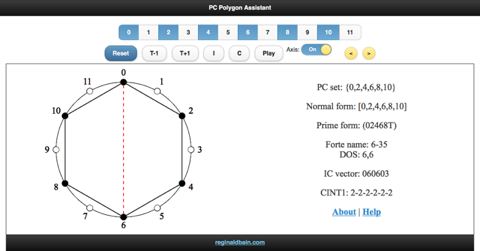
Figure 1 shows a screenshot from PC Polygon Assistant.

Figure 1. The whole-tone collection on C

Students enter pitch classes via the 12 pitch class (pc) buttons (0-11) at the top of the interface. The circular pitch-class clockface diagram is a geometric analogy for pc space (Straus 2016). In Figure 1, the current pc set is the whole-tone collection on C:

{C,D,E,F#,G#,Bb}

The fixed-zero integer notation [C=0] for this pc set is {0,2,4,6,8,10}, whose normal form (Rahn 1980) is:

[0,2,4,6,8,10]

The polygon diagram is created by connecting the adjacent pitch classes in the set using straight-line segments. For sets with 3 through 12 notes, inclusive, the app will draw an inscribed convex polygon. The style of this diagram follows conventions established in Gottfried Toussaint's The Geometry of Rhythm (Toussaint 2013) so that each pc set is isomorphic (Pressing 1983) to a 12-pulse rhythmic timeline. The pc set's prime form under Tn/TnI, Forte name, ic vector and degrees of symmetry (DOS) are also listed. The program also allows students to explore the fact that transposition (Tn) is isomorphic to geometric rotation, and inversion (I) is isomorphic to geometric reflection (Tymoczko 2011). Four transformation buttons (T-1, T+1, I, and C) allow the user to visualize the effects of transposition, inversion, and the complement relation in pc space. The T-1 and T+1 buttons will tranpose the set down and up one semitone, respectively. The I button reflects the current set about the 0/6 inversional axis (the red dotted line shown in Figure 1). The C button will calculate and display the literal complement of the current pc set. Finally, the cyclic interval array of the prime form (CINT1) is displayed. CINT1 is an ordered listing of the prime form's adjacent intervals which are isomorphic to the lengths of the sides of the polygon (Morris 1987). For more information, see the documentation.

Note: The links to geometric definitions will take take you to Wikipedia

Tools

• Scalable Vector Graphics (SVG)
  A markup language for 2D graphics applications and images W3C: <http://www.w3.org/Graphics/SVG/>

• WebAudio API
  A high-level JavaScript API for processing and synthesizing audio in the browser <http://www.w3.org/TR/webaudio/>
  Web Audio Working Group: <http://www.w3.org/2011/audio/>

• jQuery Mobile: A touch-optimized Web framework
  <http://jquerymobile.com>

• jQuery: A JavaScript library that makes event handling, animation, etc. simpler
  <http://jquery.com>

• Tone.js by Yotam Mann A web audio framework for making interactive music in the browser
  <http://github.com/Tonejs/Tone.js>

• Tune.js by Andrew Bernstein & Ben Taylor A web audio tuning library of microtonal and just intonation scales
  <http://github.com/abbernie/tune>

• NexusUI by the LSU Experimental Music and Digital Media Program
  A JavaScript toolkit of HTML5 audio interfaces in the browser
  <https://nexus-js.github.io/ui/>

• MAMP: My Apache - MySQL – PHP: A localhost server for OS X & Windows
  <http://www.mamp.info>

Documentation and Tutorials

Aldunate, Joaquín. 2016. "Web Audio API: Why Compose When You Can Code?" Toptal Engineering Blog. Available online at: <http://www.toptal.com/web/web-audio-api-tutorial>.

Jenkov.com. 2016. SVG Tutorial. Available online at: <http://tutorials.jenkov.com/svg/>.

Mozilla Developer Network. 2016. SVG Documentation. Available online at: <https://developer.mozilla.org/en-US/docs/Web/SVG>.

_______________________. 2016. Web Audio API Documentation. Available online at: <https://developer.mozilla.org/en-US/docs/Web/API/Web_Audio_API>.

References

Allison, Jesse, William Conlin, Daniel Holmes, Yemin Oh, and Ben Taylor. "Simplified Expressive Mobile Development with NexusUI, NexusUp and NexusDrop." NIME 2014: International Conference on New Instruments for Musical Expression Proceedings. London, England. Available online at: <https://www.nime.org/proceedings/2014/nime2014_480.pdf>.

Bernstein, Andrew and Benjamin Taylor. 2016. "Tune.js: A Microtonal Web Audio Library." 2nd Web Audio Conference (WAC) Proceedings. Atlanta: GA TECH. Available online at: <http://webaudioconf.com/_data/papers/pdf/2016/2016_27.pdf>.

Eisenberg, J. David and Amelia Bellamy-Royds. 2014. SVG Essentials, 2nd ed. Sebastopol, CA: O'Reilly Media.

Keith, Michael. 1991. From Polychords to Polya: Adventures in Musical Combinatorics. Princeton: Vinculum Press.

Mann, Yotam. 2015. "Interactive Music with Tone.js." 1st Web Audio Conference (WAC) Proceedings. Paris, France: IRCAM & MOZILLA. Available online at: <https://wac.ircam.fr/pdf/wac15_submission_40.pdf>. {IRCAM}

Morris, Robert. 1987. Composition with Pitch Classes. New Haven: Yale University Press.

Pressing, Jeff. 1983. "Cognitive Isomorphisms Between Pitch and Rhythm in World Musics: West Africa, the Balkans and Western Tonality." Studies in Music 17 (1983): 38–61.

Rahn, John. 1980. Basic Atonal Theory. New York: Longman.

Smus, Boris. 2013. Web Audio API. O'Reilly Media. Sebastopol, CA.

Straus, Joseph N. 2016. Introduction to Post-Tonal Theory, 4th ed. New York: Norton.

Toussaint, Godfried T. 2013. The Geometry of Musical Rhythm: What Makes a "Good" Rhythm Good? Boca Raton, FL: CRC Press.

Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press.