Use theTable of Contents (above, right) to skip to any section of this Help File. The 'Top' link at the end of each section will bring you back to the Table of Contents.

1. Introduction

Twelve-Tone Assistant is a web-based software app that performs basic 12-tone operations and generates matrices useful in the analysis and composition of twelve-tone music including the well-known Babbitt Square or 12x12 matrix.The app was designed for undergraduate music theory students. Students can expore the basic structural properties of a series, or check their answers to textbook/workbook exercises. The app has many functions that will only be of interest to the 12-tone novice. For example, it can can convert between pc letter-name and integer notation at the touch of a button. When labeling series forms, students can work in either fixed-zero notation (Straus 2005) or movable-zero notation (Kostka and Payne 2008). The app can convert between the two labeling systems at the touch of a button. When used in conjunction with a word processor, the app's text output may be exported (via copy-and-paste) into homework assignments, term papers, and the like. Matrices can be produced as space-delimited output (useful for viewing in an HTML textarea), comma-delimited output (useful for creating tables in a word processor like Microsoft Word), or as HTML output (useful for viewing in an HTML window, or producing HTML source code that may be posted on a website).

A working knowledge of basic twelve-tone theory is required to use Twelve-Tone Assistant. Students who require a brief introduction to the subject are directed to Straus 2005 Chapter 5.

2. Feature Summary

Enter a 12-tone series and Twelve-Tone Assistant can:

1. Display the 48 forms of the series using pitch-class letter name, integer or staff notation.
2. Label series forms using fixed-zero [C=0] or movable-zero (first pc of the series equals zero) system.
3. Report the interval succession (opci and ic) for all P, R, I or RI forms of the series.
4. Report the set class-membership of the discrete trichords, discrete tetrachords, and discrete hexachords.
5. Determine if a series is a derived series, an all-combinatorial series, or an all-interval series.
6. Determine hexachordally combinatorial (P-comb., R-comb., I-comb., or RI-comb.) with respect to the prime ordering.
7. Produce the following matrices: Babbitt Square (12x12 matrix), P-form Array, I-form Array, Rotational Array, Four-Part Array, and Permutational Array

3. Getting Started

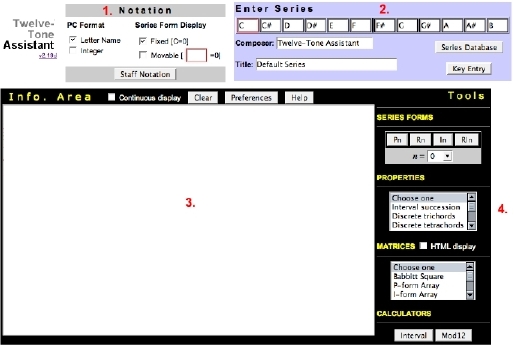
Fig. 1 shows Twelve-Tone Assistant's top-level interface and default program settings.

Fig. 1. Twelve-Tone Assistant's top-level interface and default settings.

Twelve-Tone Assistant human interface is divided four areas. Numbered 1-4 in Fig. 1, these are briefly introduced below.

1. Notation Area

The Notation Area controls how Twelve-Tone Assistant displays pitch classes and labels series forms. Choose pitch-class (pc) letter name vs. integer display. When Fixed [C=0] is checked, C is the reference pc (see section 4.21). When Movable [X=0] is checked, where X is the first pitch class of the series, pc X is the reference pc (see section 4.22). Pitch classes may also be displayed using staff notation (see section 4.4). See section 4. The Notation Area for more information.

2. Enter Series Area

The Enter Series Area has twelve order-position form elements that define the current 12-tone series. A series may be entered using pc letter names or fixed-zero pc integers (C=0, C#/Db=1, D=2, etc.). The series may also be entered via the Series Database Window (see section 3.2), or via the 1-octave keyboard in the Key Entry Window (see section 3.3). See section 3. Entering a Series for more information.

3. Info. Area

By default, Twelve-Tone Assistant sends all output to the Information Area: the large white HTML textarea that occupies the bottom-left portion of the main interface. Your browser's preferences must be configured to display a monospace font for text be vertically aligned in this area, See section 6. Vertical Alignment of Data for more information.

Twelve-Tone Assistant can produce space-delimited (default) or comma-delimited output. Comma-delimited output is useful for importing data into tables, spreadsheets and databases. For example, comma-delimited output may be imported into a Microsoft Word table (see section 7.38) or Excel spreadsheet. See section 5. The Information Area for more information.

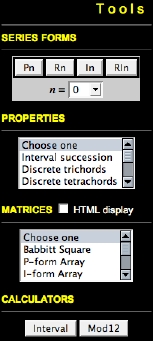
4. Tools Area

The Tools Area has four modules: a. Series forms, b. Properties, c. Matrices and d. Calculators. The first three modules produce reports in the Info. Area, whereas the calculators run as independent apps in pop-up windows. Each module is briefly described below. See section 7. The Tools Area and 8. Calculators for more information.

a. Series Forms

The Series Forms module displays the 48 forms of the series that are produced by the basic operations P, R, I, and RI. Series forms are notated and labeled using the Notation Area's current settings. See section 7.1 Series Forms for more information.

Please note that Twelve-Tone Assistant's Preferences may be configured to display order numbers and/or the interval succession along with a given series form. See section 9. Preferences for more information.

b. Properties

The Properties module identifies important structural features of the series. You can list the series's: interval succession (opci and ic), the set-class membership of the discrete trichords, tetrachords and hexachords; and test the series for the following structural properties: derivation (trichordal or tetrachordal), hexachordal combinatoriality, all-combinatoriality and the all-interval series property. See section 7.2 Properties for more information.

c. Matrices

The Matrices module can produce twelve-tone matrices in the Info. Area or in a new HTML window. Matrices include a traditional 12 x 12 matrix (called a Babbitt Square), P-form Array, I-form Array, Rotational Array, Four-Part Array and Permutational Array. See section 7.3 Matrices for more information.

d. Calculators

The Calculator module provides access to two pedagogically-oriented calculators: the Interval Calculator and Mod 12 Calculator. See section 8.Calculators for more information.

 

3. Entering a Series

Fig. 2 shows the Enter Series Area with the series from Schoenberg's Fourth String Quartet, Op. 37 loaded into its twelve order-position elements.

Fig. 2. The Enter Series Area.

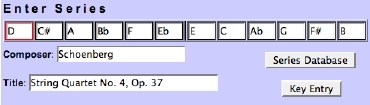
We will use the series from Schoenberg's Op. 37 throughout this help module to demonstrate the program's features.The series listed in the Enter Series Area is called the current series. Twelve-Tone Assistant provides three ways to enter the current series. You can:

1. Type the pitch classes of the series into the Enter Series Area's twelve order-position elements

2. Select a series from the Series Database (see section 3.2)

3. Use the 1-octave keyboard or pc checkboxes in the Key Entry Window to enter the series (see section 3.3)

All three entry methods are discussed below.

3.1 The Enter Series Area's Twelve Order-Position Elements

You can enter the current series by typing its pitch classes into the Enter Series Area's twelve order-position elements in left-to-right order (order numbers: 1-12, or 0-11). Note the thin bold divider that divides the series into two hexachords. Note, too, the Composer and Title fields (see section 3.4), as well as the Series Database (see section 3.2) and Key Entry (see section 3.3) buttons.

3.11 PC Entry Format

Pitch classes may be entered in the Enter Series Area using the following two pc formats:

1. Letter name
2. Integer

Integers must be fixed-zero pc integers. For a list of legal pc symbols, see section 3.6 PC Symbols. Please note that the Series Form Display options do not affect series entry.

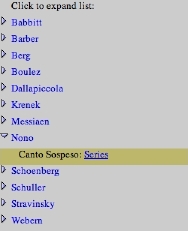
3.2 The Series Database

The second way to enter the current series is to select it from the Series Database. Click the Series Database button (see Fig. 2) to load the Series Database Window which is shown in Fig. 3.

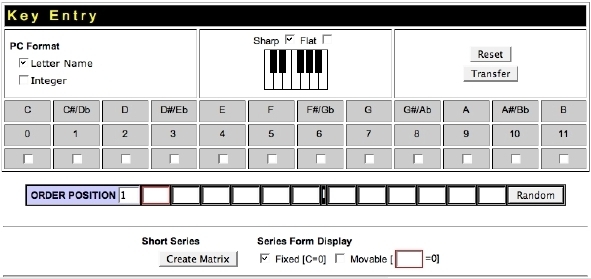
3.3 The Key Entry Window

The third way to enter the current series is to use the 1-octave keyboard or pc checkboxes provided in the Key Entry Window which is shown in Fig. 4.

Fig. 4. The Key Entry Window.

Click the Key Entry button in the Enter Series Area (see Fig. 2) to load the Key Entry Window. Like the Enter Series Area, this window contains twelve order-position elements, however, you cannot type into these form elements. Rather, pitch classes are entered by clicking on the 1-octave keyboard or pc checkboxes. When you enter a pc, the order position counter (light blue) is automatically incremented, and the next order position element is brought into focus so you can select the next pc.

3.31 PC Format and Series Form Display Settings

Notice that they Key Entry Window has its own independent PC Format and Series Form Display settings. When the Key Entry Window loads, Twelve-Tone Assistant will match the Key Entry Window's settings to those in the Notation Area (see section 4).

3.32 Removing a PC

If you accidentally enter the wrong pc, you can remove it by immediately clicking on the same piano key or pc checkbox again before you enter another pc. When you remove a pc in this manner, the order position counter is decremented and the previous order position element is brought into focus so you can select the correct pc.

3.33 Reset

Click the Reset button to erase all entries and start the entry process over.

3.34 Transfer

When all twelve pitch classes have been successfully entered into the order position elements, you will receive the following message confirming successful entry of the series:

Click the Transfer button to copy the series into the Enter Series Area and then close the Key Entry Window.

3.35 Generating a Random Series

Click the Random button to generate a random series. Any previous pc entries will be erased. Click the Transfer button to copy the random series into the Enter Series Area.

3.36 Create Matrix

See section 7.37 Short-Series Matrix for more information.

3.4 The Composer and Title Fields

You can associate a composer name and title with the current series. The Composer field is limited to a maximum 20 characters. The Title field is limited to a maximum 30 characters. The default composer is "Twelve-Tone Assistant" and the default title is "Default Series."

3.5 Default Series

When you launch Twelve-Tone Assistant, the following default series is loaded into the twelve order-position elements in the Enter Series Area:

C C# D D# E F F# G G# A A# B

This series was chosen because it is the normal form of the aggregate.

3.6 PC Symbols

Twelve-Tone Assistant uses the following 12 pc integer and 21 pc letter name symbols for input and output:

Fig. 5. PC symbols.

PC Integers [C=0]

0

1

2

3

4

5

6

7

8

9

10

11

PC Letter Names (Sharp)

B#

C#

D#

E#

F#

G#

A#

PC Letter Names (Natural)

C

D

E

F

G

A

B

PC Letter Names (Flat)

Db

Eb

Fb

Gb

Ab

Bb

Cb

Each column in Fig. 5 represents one of the twelve pitch classes. The sharp symbol is the '#' symbol (shift-3). The flat symbol is the 'b' symbol (lowercase b). Double-sharps and double-flats are not currently recognized. Single character substitutions for '10' and '11' are available when displaying output. See section 9.1 10/11 Substitution for more information.

The Notation Area shown in Fig. 6 controls how Twelve-Tone Assistant notates pitch classes and labels series forms.

Fig. 6. The Notation Area.

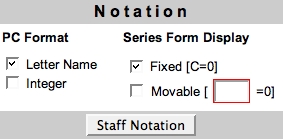
You can choose between Letter name and Integer pitch-class formats. You can also choose between fixed-zero and movable-zero series form display. When Fixed [C=0] series form display is selected, C is the reference pc (abbreviated [C=0]), that is:

C=0, C#/Db=1, D=2, D#/Eb=3, E=4, F=5, F#/Gb=6, G=7, G#/Ab=8, A=9, A#/Bb=10, B=11

Indicated by a red box in Fig. 6 (see also Figures 2 and 4), the reference pc is always given using pc letter name notation. When Movable [X=0] series form display is selected, the first pitch class of the series is the reference pc. Note that the reference pc is enclosed within a red box (see Figures 2 and 6, see also Figure 4). For example, if D is the first pitch class of the series, the reference pc is D (abbreviated [D=0]) and:

D=0, D#/Eb=1, E=2, F=3, F#/Gb=4, G=5, G#/Ab=6, A=7, A#/Bb=8, B=9, C=10, C#/Db=11

Pitch classes can also be displayed using staff notation (see section 4.4). The four checkboxes in Fig. 6 essentially produce four notational styles. See section 4.3 Four Notational Styles for more information.

4.1 PC Format

When the Notation Area's Letter Name option is checked, Twelve-Tone Assistant uses pc letter names for input (in the Enter Series Area) and output (in the Info. Area & HTML windows). When the Integer option is checked, it uses fixed-zero pc integers for input and output. The series in the Enter Series Area (see Fig. 2) is immediately updated to the current format.

Let's use the series from Schoenberg's Fourth String Quartet, Op. 37 to demonstrate the difference between the two formats. The series from Op. 37 is given below using staff notation, pc letter name notation, and fixed-zero pc integer notation [C=0]:

Letter Name: D C# A Bb F Eb E C Ab G F# B

Integer: 2 11 9 10 7 5 4 0 8 7 6 11

4.2 Series Form Display

In the analysis of twelve-tone music, some authors employ a fixed-zero system to label series forms while others employ a movable-zero system. Straus (2005) and Kostka (2005) employ the former, while Kostka and Payne (2008) and Lester (1989) use the latter. Twelve-Tone Assistant allows you to convert between the two systems.

4.21 Fixed [C=0]

When the Fixed [C=0] series form display option is checked, Twelve-Tone Assistant assumes that:

C=0, C#/Db=1, D=2, D#/Eb=3, E=4, ..., B=11

and that the index x of all Px (also called P_x) and Ix (also called I_x) series forms is equal to the first pc of the given series form. The prime form of the series from Op. 37,

D C# A Bb F Eb E C Ab G F# B

is labeled P2, because its begins with D which is pc 2. The inverted form of the series,

G Ab C B E F# F A C# D Eb Bb

whose equivalent fixed-zero pc integer notation is,

7 8 0 11 4 6 5 9 1 2 3 10

is labeled I7, because it begins with G which is pc 7. Note that the index x of all Rx and RIx forms does not agree with the first pc of the series form, for example,

10 3 2 1 9 5 6 4 11 0 8 7

the retrograde of I7 above, is labeled RI7.

4.22 Movable [X=0]

When the Movable [X=0] series form display option is checked, Twelve-Tone Assistant assumes that the first pc of the current series is the reference pc. Note that the reference pc is indicated by a red box (see Figures 2 and 6, see also Fig. 4). Again, using the prime form of the series from Op. 37,

D C# A Bb F Eb E C Ab G F# B

Twelve-Tone Assistant assumes that D is the reference pc (abbreviated [D=0]), and that:

D=0, D#/Eb=1, E/Fb=2, F=3, F#/Gb=4,..., B=11

When the Movable [X=0] option is checked, the prime form of the series,

D C# A Bb F Eb E C Ab G F# B

is labeled P0 (rather than P2), whose equivalent fixed-zero pc integer notation is:

0 11 7 8 3 1 2 10 6 5 4 9

4.3 Four Notational Styles

The Notation Area's PC Format and Series Form Display options combine to create four notational styles: (1) Letter Name Notation [C=0], (2) Letter Name Notation [X=0], where X is any pc, (3) Integer Notation [C=0], and (4) Integer Notation [X=0], where X is any pc. The following table compares the four styles using the series from Op. 37:

Style	Style Abbreviation	PC Format	Series Form Display	Ref. PC	Notation for P0
1.	Letter Name Notation [C=0]	Letter name	Fixed [C=0]	[C=0]	C B G Ab Eb C# D Bb F# F E A
2.	Letter Name Notation [X=0]	Letter name	Movable [X=0]	[D=0]	D C# A Bb F Eb E C Ab G F# B
3.	Integer Notation [C=0]	Integer	Fixed [C=0]	[C=0]	0 11 7 8 3 1 2 10 6 5 4 9
4.	Integer Notation [X=0]	Integer	Movable [X=0]	[D=0]	0 11 7 8 3 1 2 10 6 5 4 9

These style abbreviations are used in the Info. Area when Twelve-Tone Assistant's Header preference (see section 9.32) is on, and in the footer information of HTML matrices (see section 7.3). Note that when using styles 3 and 4 the integer representations for P0 are equivalent, only the reference pc changes. Also note that the Fixed [C=0] and Movable [X=0] options will produce the same results for any series that begins with pc 0.

4.4 Staff Notation

Click the Notation Area' s Staff Notation button (see Fig. 6) to bring up the Staff Notation Window shown in Fig. 7.

Fig. 7. The Staff Notation Window.

When this window loads, the P0 form of the series is notated using the Notation Area's current Series Form Display setting. In Fig. 7, the current setting is Movable [D=0]. Use the Choose form menu (lower right) to display any one of the forty-eight forms of the series. Your selection is confirmed to the left of the staff. In most browsers, order numbers will appear in the Staff Notation Window's Assistance Area as you scroll over the members of the series. The interval succession is listed below the staff using ordered pitch-class intervals (opci) and interval classes (ic).

 

5. The Information Area

Twelve-Tone Assistant sends all text output to the Information Area (abbreviated Info. Area) shown in Fig. 8.

Fig. 8. The Info. Area.

In Fig. 8, the current notational style is Letter Name Notation [C=0]. In order for text output to appear vertically aligned in this area, your browser's preferences must be configured to display a monospace font. See section 6. Vertical Alignment of Data for more information. Twelve-Tone Assistant can produce space-delimited (default) or comma-delimited output in the Info. Area. Comma-delimited output is useful for importing data into tables, spreadsheets and databases, for example, comma-delimited output can be used to import matrix data into a Microsoft Word table (see section 7.38).

5.1 The TEXTAREA Object

The Info. Area is created with a textarea object, an HTML form element designed to handle multiple-line text input (not output). The size of the Info. Area, 80 columns by 30 rows, was chosen to accommodate Twelve-Tone Assistant's largest matrix. Unfortunately, it is impossible to format the data in a textarea object. Nonetheless, it is useful for presenting text data that will ultimately be transferred to another program (via traditional copy and paste techniques) for further formatting and typesetting. In order to get data to vertically align in the Info. Area, you must configure your browser's preferences to display a monospace font. See section 6. Vertical Alignment of Data for more information.

5.2 Delimited Output

Twelve-Tone Assistant can produce space-delimited (default) or comma-delimited output in the Info. Area. Comma-delimited output is useful for importing data into another program. The commas tell the external program where each cell, field, etc. begins. See section 9. Preferences for more information about how to generate comma-delimited output in the Info. Area.

5.3 Continuous Display Option

Twelve-Tone Assistant automatically clears any previously displayed data in the Info. Area before it reports new data. When the Continuous Display option is checked, however, this automatic clear feature is turned off. This feature can be used to generated running reports of data. In Fig. 8, for example, series forms P2 and P7 are presented in the Info. Area using the Continuous Display Option to examine the property of hexachordal combinatoriality. See section 7.25. Hex. Comb. At for more information about hexachordal combinatoriality.

5.4 Using The Info. Area as a Workspace

If you wish, you can freely use the Info. Area as a workspace. You can type new data into it, rearrange the order of its contents, change pitch classes, and so forth. Please note, however, that Twelve-Tone Assistant only keeps track of the data that it generates, so be sure to save any edits you make to another application before you execute a program function that writes data to the Info. Area. The easiest way to do this is to copy and paste your data to another application, for instance, Microsoft Word.

5.5 Clear

Click the Clear button to clear the Info. Area.

5.6 Preferences

Click the Preferences button to bring up TTA's Preferences window. See section 9. Preferences for more information.

5.7 Help

Click the Help button to load this document in a new HTML window.

6. Vertical Alignment of Data

In order to get multiple lines of data to vertically align in the Info. Area, as shown in all of the examples below, you must configure your browser to display a monospace font in textarea objects (see 5.1 section 5.1). A monospace font like Courier and point size of 13 are recommended. Click here for step-by-step instructions for the Netscape 7.2 browser. The procedure for configuring this preference is similar for most browsers.

Fig. 9. The Tools Area.

7. The Tools Area

The Tools Area shown in Fig. 9 provides access to most of the program's features. It has four modules:

1. Series forms

2. Properties

3. Matrices

4. Calculators

Each button and menu item in the Tools Area is described below, along with sample output for the series from Schoenberg's Fourth String Quartet, Op. 37:

D C# A Bb F Eb E C Ab G F# B

When the series from Op. 37 is not an appropriate example, a new series will be introduced.

7.1 Series Forms

Enter n, the series form index, into the n = form element and click the Pn, Rn, In or RIn button to display the corresponding series form. The series form will be displayed in the Info. Area using the current settings in the Notation Area. For example, to display P7 in the Info. Area, enter 7 into the n = form element and click the Pn button. The following table summarizes the four possible outcomes.

Style	Series Form Display	PC Format	Ref. PC	Notation for P7
1.	Fixed [C=0]	Letter Name	[C=0]	G G# A A# B C C# D D# E F F#
2.	Movable [X=0]	Letter Name	[D=0]	A Ab E F C Bb B G Eb D C# F#
3.	Fixed [C=0]	Integer	[C=0]	7 6 2 3 10 8 9 5 1 0 11 4
4.	Movable [X=0]	Integer	[D=0]	7 6 2 3 10 8 9 5 1 0 11 4

To display more than one series form at a time in the Info. Area, use the Continuous Display option. See section 5.4. Continuous Display Option for more information.

7.11 Series Form Symbols

Series form symbols range from two to four characters in length. Twelve-Tone Assistant uses the following 48 symbols in the Info. Area:

P0-P11, R0-R11, I0-I11 and RI0-RI11

Note that series form symbols that juxtapose an 'I' and a '1', for example, compare R10 and RI0, can be notoriously difficult to distinguish from one another. The use of subscript notation for the series form index is often used to alleviate this problem. Subscript notation produces the following 48 series form symbols:

P₀-P₁₁, R₀-R₁₁, I₀-I₁₁ and RI₀-RI₁₁

Subscript notation is available via the HTML Display option. See section 7.36 HTML Display for more information.

7.2 Properties

The Properties module is designed to help you identify important structural properties of the series. Choose an item from the Properties menu to produce a report in the Info. Area.

7.21 Interval Succession

In Interval succession option displays the interval succession for the prime form of the series in terms of ordered pitch-class intervals (opci) and interval classes (ic). For Op. 37:

By configuring the program's Preferences, you can display the opci and ic succession for any series form. This method also allows for alignment of the interval succession with the series form. For example, for the I0 form of the series from Op. 37, which is given in Letter Name Notation [C=0]:

See section 9. Preferences for more information. Please note that the interval succession is also displayed in the Staff Notation Window. See section 4.4 Staff Notation for more information.

7.22 Discrete Subsets

Twelve-Tone Assistant can report the set class membership (prime form and Forte name) for each of the discrete subsets of the series. Discrete subsets divide the series into ordered segments that do not overlap. See Straus (2005) "Set Class," pp. 52-57 and "Subset Structure," pp. 192-95 for more information.

7.221 Discrete Trichords

The Discrete trichords option displays the set class membership for each of the four discrete trichords of the series. For Op. 37:

7.222 Discrete Tetrachords:

The Discrete tetrachords option displays the set class membership for each of the three discrete tetrachords of the series. For Op. 37:

7.223 Discrete Hexachords:

The Discrete hexachords option displays the set class membership for the discrete hexachords of the series. For Op. 37:

7.24 Derived Series

In a derived series, all of the discrete trichords or tetrachords belong to the same set class. Twelve-Tone Assistant reports whether or not the series is trichordally or tetrachordally derived, and if so, whether or not the derivation is ordered under the transformations P, I, R or RI. For a symmetrical series, more than one answer is possible. Twelve-Tone Assistant uses the following order of priority to select a single representative series form: 1. P, 2. I, 3. R, 4. RI. If a given generating trichord or generating tetrachord is related to more than one P-form, I-form, R-form, or RI-form, the form with the lowest index number is reported. The Op. 37 series is not a derived series. See Derived Series Examples to see the range of possible outcomes. See Straus (2005), "Webern and Derivation," pp. 217-21 for more information.

7.25 Hex. Comb. At

The principle of hexachordal combinitoriality is easy to demonstrate. The P0 and I5 forms of the series from Op. 37 are given using Letter Name Notation [D=0] in Fig. 10.

Fig. 10. Hexachordal Combinatoriality

When these two series forms are listed in counterpoint to one another, a special relationship between the hexachords becomes apparent. Notice that the first hexachord of P0 (D,C#,A,Bb,F,Eb) is equivalent to the second hexachord of I5 (F,A,C#,D,Eb,Bb). When this is the case, the first hexachords of P0 and I5 combine vertically to form the aggregate, as do the second hexachords of P0 and I5. Of course, the same relation holds for P1 and I6, P2 and I7, P3 and I8, etc., and for R0 and RI5, R1 and RI6, R2 and RI7, etc . Keep in mind that, for any series, P0 is always hexachordally combinatorial with R0.

Twelve-Tone Assistant reports all P-forms, I-forms, R-forms, and RI-forms that are hexachordally combinatorial with respect to P0. For Op. 37, it reports that the:

Please note that the same results are obtained for Fixed [C=0] and Movable [X=0] series form display notation. See Straus (2005) "Schoenberg and Hexachordal Combinatoriality," pp. 222-230 for more information.

7.26 All-comb. series

A series is all-combinatorial if it is hexachordally combinatorial with at least one of each of the following: a P, R, I and RI form. Twelve-Tone Assistant reports which forms of the series produce hexachordal combinatoriality (see the previous section) and whether or not the series is all-combinatorial. For Op. 37, it reports that:

On the other hand, for the series from Webern's Symphony, Op. 21,

A F# G Ab E F B Bb D C# C Eb

Twelve-Tone Assistant reports that:

See Straus (2005) "Schoenberg and Hexachordal Combinatoriality," pp. 222-230 for more information.

7.26 All-interval series

A series is an all-interval series if each opci in its interval succession is represented only once. Twelve-Tone Assistant reports the opci succession and whether or not the series is an all-interval series. For Op. 37, it reports that:

On the other hand, for Series C from Berg's Lyric Suite,

F E C A G D Ab Db Eb Gb Bb B

it reports that:

See Morris (2001) "Types of Rows," pp. 151-53 for more information.

7.3 Matrices

Twelve-Tone Assistant can produce a variety of matrices associated with the composition and analysis of twelve-tone music. Matrix data is sent to the Info. Area as space-delimited (default) or comma-delimited output. Comma-delimited output is useful for importing matrix data into a word processing programs where the matrix data be subjected to further formatting and typesetting.The notational style of the matrix is determined by the Notation Area's current settings (see section 4). The HTML Display option (see Fig. 9) directs matrix output to a new HTML window rather than the Info. Area. Series form index subscript notation is available in HTML windows. See section 9. Preferences for more information.

The Matrices menu has six options: 1) Babbitt Square, (2) P-form Array, (3) I-form Array, (4) Rotational Array, (5) Trichordal Array, (6) Permutational Array. What is more, the Key Entry Window can be used to produce a short-series matrix. See section 7.37 Short Series Matrix for more information.

7.31 Babbitt Square: A traditional 12x12 matrix listing the all forty-eight series forms: P-forms are read in left-to-right order; R-forms right-to-left; I-forms top-to-bottom; and RI-forms bottom-to-top. For Op. 37:

See Straus (2005), pp. 186-88 for more information.

7.32 P-form Array: A listing of the twelve P-forms and R-forms of the series: P-forms are read in left-to-right order; R-forms are read right-to-left.

7.33 I-form Array : A listing of the twelve I-forms and RI-forms of the series: I-forms are read in left-to-right order; RI-forms are read right-to-left.

7.34 Rotational Array: A Stravinsky-style rotational array based on the two discrete hexachords of the series. For example, for Series A from Stravinsky's Requiem Canticles,

F G D# E G F# C# B C D A G# A

Twelve-Tone Assistant will generate the following the following rotational array:

The two hexachords of the series are independently subjected to Stravinsky's rotation-transposition process yielding two sets of six (labeled I-VI) rotation-transposition forms .See Straus (2005) "Stravinsky and Rotational Arrays," pp. 231-34 for more information.

7.35 Permutational Array: A Brindle-style permutational array listing the nine (labeled a-j) every-other-note permutations of the series. For example, for Twelve-Tone Assistant's Default Series, which is given using Integer [C=0] notation below,

0 1 2 3 4 5 6 7 8 9 10 11

it will generate the following the following permutational array:

See Brindle (1966) "Permutations and Other Variants of a Series," pp. 154-57 for more information.

7.36 HTML Display

Check the HTML Display option to direct matrix output to a new HTML window rather than the Info. Area. Fig. 11 shows an HTML version of a Babbitt Square for Op. 37.

Fig. 11. HTML version of a Babbitt Square.

Note the footer information that appears at the bottom of all HTML matrices listing: composer, title, matrix type, and notational style.

7.37 Short-Series Matrix

See Short-Series Matrix for more information.

7.38 Importing Matrix Data into a Microsoft Word Table

Here's a pdf tutorial that explains how to import matrix data into a Microsoft Word table.

8. Calculators

Twelve-Tone Assistant's two calculators are described below.

8.1 Interval Calculator

Shown in Fig. 12, the Interval Calculator reports the 1. ordered pitch interval, 2. unordered pitch interval, 3. ordered pitch-class interval, 4. interval class (also called unordered pitch-class interval), and 5. traditional tonal interval for any two pitches between C1 and B6 inclusive.

Fig. 12. The Interval Calculator.

Use the 6-octave piano keyboard to enter Pitch 1 and Pitch 2. Note that middle C, or C4, is the fourth C key from the left. When you position the cursor over a key in the Netscape browser, the pitch, MIDI pitch number, and pitch-class integer [C=0] appear in the Assistance Area as shown in Fig. 12. Click on the piano keyboard to enter Pitch 1 and Atonal Assistant will automatically advance to the Pitch 2 field, and vice versa. Click the Interval Calculator's Calculate button to return the five interval types. Click the Reset button to clear all fields and start the entry process over.

8.12 Traditional Tonal Interval

Traditional tonal interval names are reported as simple intervals, that is, up or down, within the octave.

8.2 Mod 12 Calculator

The Mod 12 Calculator shown in Fig. 13 resembles a traditional calculator, however, it performs Modulo 12 (abbreviated Mod 12) addition, subtraction and multiplication.

Fig. 13. The Mod 12 Calculator.

The Mod 12 (n) button can be used to return the Mod 12 equivalent of any integer. To enter a negative number, click the minus key '-' before you enter a number. A few sample calculations should serve to demonstrate its basic function and usefulness for pitch-class interval calculation.

10 + 2 = 0
2 + 2 = 4
11 + 4 = 3
4 - 6 = 10
-3 + 2 = 11
5 - 10 = 7
3 * 4 = 0

Please note that all operations are performed on the two previous entries, that is, you cannot perform operations like 3 + 3 + 3 = 9 which require more than two operands.

9. Preferences

The Preferences Window and its default settings are shown in Fig. 14.

Fig. 14. The Preferences Window.

The settings in the Preferences Window affect the display of data in the Info. Area and in HTML matrices. It is divided into three areas: 1. 10/11 Substitution, 2. Info. Area Options, and 3. HTML Matrix Options. Each preference is discussed below.

9.1 10/11 Substitutions

Of the twelve pc integer symbols (0-11 inclusive), only 10 and 11 are two-characters in length. Theorists have traditionally substituted a one character symbol for pc integers 10 and 11. A variety of substitutions have been proposed. Twelve-tone Assistant offers the following four 10/11 character substitutions:

9.11 t=10, e=11

The symbol 't' is substituted for '10'. The symbol 'e' is substituted for '11'.

9.12 T=10, E=11

The symbol 'T' is substituted for '10'. The symbol 'E' is substituted for '11'.

9.13 a=10, b=11

The symbol 'a' is substituted for '10'. The symbol 'b' is substituted for '11'.

9.14 A=10, B=11

The symbol 'A' is substituted for '10'. The symbol 'B' is substituted for '11'.

These preferences affect all program features that involve the display of pc integers. Please note that 10/11 substitution also affects the indices of series form symbols. For example, if the t=10, e=11 preference is on, Pt will be substituted for P10, Pe will be substituted for P11, and so forth as demonstrated in the example below:

9.2 Info. Area Options

The following preferences affect how Twelve-Tone Assistant displays data in the Info. Area.

9.21 Delimiter

Twelve-Tone Assistant offers two types of delimiters: 1. Spaces, or 2. Comma. The former preference produces space-delimited output and the latter produces comma-delimited output. Comma-delimited output affects the display of series forms (see section 7.1) and matrices (see section 7.3).

9.211 Spaces

When the Spaces preference is checked, each series form member and matrix cell is separated by spaces as shown below:

Note that each cell requires at least four characters if the matrix is to align. This is because the series form symbols RI10 and RI11 require four characters. Extra spaces are added after each pc and series form symbol as necessary. See section 6. Vertical Alignment of Data for more information about configuring your browser to use a monospace font.

9.212 Comma-Delimited Output

If the Comma preference is checked, each series form member and matrix cell is separated by a comma so that the data can easily be imported into other programs as respectively shown in the examples below:

---

See section 7.38 Importing Matrix Data into a Microsoft Word Table for more information.

9.32 Header

When the Header preference is on, Twelve-Tone Assistant reports the composer, title, and notational style (see section 4.3), where appropriate, above all Info. Area reports. You may want to turn the header off at times so you can create a custom report using the Continuous Display option. See section 5.3 Continuous Display Option for more information.

9.33 OPCI

When the OPCI preference is on, Twelve-Tone Assistant displays the interval succession using ordered pitch-class intervals below all series forms (see Fig. 15).

9.34 IC

When the IC preference is on, Twelve-Tone Assistant displays the interval succession using interval classes below all series forms (see Fig. 15).

9.35 Order Numbers

When this preference is on, Twelve-Tone Assistant displays order numbers above all series forms (see Fig. 15).

9.36 Order Number Format

When the Order Numbers preference is on, Twelve-Tone Assistant allows you to choose between two order number formats: 1-12, or 0-11 (see Fig. 15).

Fig. 15. The P0 series form displayed in the Info. Area with the Order Numbers (0-11),
OPCI and IC preferences turned on.

9.4 HTML Matrix Options

9.41 Subscript Notation

When the Subscript Notation preference is on, Twelve-Tone Assistant uses subscript notation for series form symbols in all HTML matrices. For example, P₀ is substituted for P0, R₁₀ for R10, RI₀, for RI0, and so forth. See sections 7.11 Series Form Symbols and 7.36 HTML Display Option for more information.

10. Feature Definitions

A working knowledge of twelve-tone theory is required to use Twelve-Tone Assistant. The program's features are consistent with the terms, definitions and symbols employed in Kostka and Payne (2008), which adopts the notation found in Straus (2005). Precise definitions of the following terms (listed in alphabetical order) may be found in Straus (2005) on the following pages:

Aggregate, p. 94
All-combinatorial series, pp. 224-25
All-interval series, p. 193
Basic operations (P, R, I, RI), pp. 183-85
Derived series, p. 217-21
Discrete subset set-class membership , pp. 192-95
Discrete trichords, tetrachords and hexachords, p. 193
Forte name, p. 59
Forty-eight series forms, pp. 185-86
Hexachordal combinatoriality, pp. 222-30
Integer notation, pp. 4-5
Intervals, pp. 6-13
Letter name notation, p. 3
Matrices, pp. 186-88, 231-34, 240-42.
Mod 12, pp. 5-6
Normal form, pp. 35-38
Prime form, pp. 57-59
Series form index, pp. 183-85
Series forms, pp. 183-86
Set class, pp. 52-57
Twelve-tone series, p. 182
Z-relation, pp. 91-93

The terms fixed-zero and movable-zero notation are borrowed from Lester (1989), p. 67.

11. Troubleshooting

Click here to see a screenshot of Twelve-Tone Assistant's user interface as it appears in the Netscape 7.2 browser. If the interface you get when you launch the program does not resemble this one, or if the program is not functioning as you think it should, please try the following:

1. If you can't see all of Twelve-Tone Assistant's interface, resize the browser window as necessary.
2. If Atonal Assistant will not load, check your browser preferences to be sure that JavaScript is enabled.
3. If the Series Database Window, Staff Notation Window, HTML matrix windows, Interval Calculator, or Mod 12 Calculator will not load, check your browser preferences to be sure that Block Pop Up Windows is set to off.
4. If Atonal Assistant loads but does not seem to be functioning correctly, click your browser's Reload button while holding down your computer's shift key. This will force the entire program and all of its media assets to reload from the server.
5. If you mistype your User Name or Password and cannot successfully log in to the program, quit your browser, restart it, and try again.
6. If data does not vertically align in the Info. Area, see section 6. Vertical Alignment of Data.

If these steps do not fix the problem, please send an e-mail message to the author at rbain@mozart.sc.edu. Be sure to include information about your computer, operating system, and browser version, along with your description of the problem. Click here to run a script that automatically identifies your browser and operating system. Please copy and paste this information into any e-mail message you send the author.

12. References

Brindle, Reginald Smith. Serial Composition. New York: Oxford University Press, 1966.

Castine, Peter. Set Theory Objects: Abstractions for Computer-Aided Analysis and Composition of Serial and Atonal Music. Berlin: Peter Lang, 1994.

Forte, Allen. The Structure of Atonal Music. New Haven: Yale University Press, 1973.

Goodman, Danny.The JavaScript Bible, Third Edition. New York: IDG Books, 1998.

Kostka, Stefan. Materials and Techniques of Twentieth-Century Music, 3rd ed. Upper Saddle River, NJ: Prentice Hall, 2006.

Kostka, Stefan and Dorothy Payne. Tonal Harmony: With An Introduction to Twentieth-Century Music, Sixth Edition. New York: McGraw Hill, 2008.

Lester, Joel. Analytic Approaches to Twentieth-Century Music. New York: Norton, 1989.

Morris, Robert. Class Notes for Advanced Atonal Music Theory, Volume 1. Hanover, NH: Frog Peak Music, 2001.

Rahn, John. Basic Atonal Theory. New York: Longman, 1980.

Straus, Joseph N. Introduction to Post-Tonal Theory, 3rd ed. Upper Saddle River, NJ: Prentice Hall, 2005.