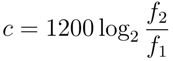Software

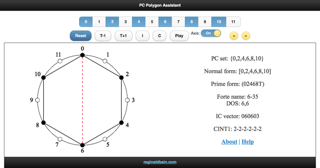
PC Polygon Assistant was created to allow my post-tonal theory students to display the polygon notation for any pitch-class set. It is a touch-optimized Web app that uses SVG to render the polygon notation. It also reports the basic structural properties of the set and allows the student to visually explore geometric analogies for transposition (T), inversion (I), and the complement relation (C) in pc space. Playback is available via Web Audio API. For more information, see the documentation (below) and my ATMI 2016 presentation.

Documentation: pdf

Current version: 2.03

Released: 2/14/22

Used in the following course: MUSC 525 Post-Tonal Theory

References: Straus 2016; Also Rahn 1980, Morris 1987, Tymoczko 2011 and Toussaint 2013

Twelve-Tone Assistant: A twelve-tone theory calculator and matrix maker

This JavaScript application performs basic 12-tone row operations and generates matrices useful in the composition and analysis of twelve-tone music.

Current version: 2.4

Released: 2/24/2017

Used in the following course: MUSC 525 Post-Tonal Theory

Reference: Straus 2016

Ratio to Cents: Allows students to convert an interval frequency ratio to cents

Ratio to Cents is a simple mobile Web app that allows students to convert an interval frequency ratio to cents on a smartphone. Built with jQuery Mobile, the program utilizes the following conversion formula:

where c is cents, and f₂ /f₁ is a pitch interval expressed as a frequency ratio. Students typically enter a frequency ratio derived from the harmonic series, or a tuning system like Pythagorean or just intonation,

e.g., 1/1, 2/1, 3/2, 4/3, 5/3, 5/4, 6/5, 9/8, 7/4, 81/64, 22/7, 81/80, etc.

and the program will report the ratio's size in cents and decimal equivalent. Decimal values (e.g., 1.618/1, 3.14/2, etc.), reciprocal frequency ratios (e.g., 1/2, 2/3, 3/4, etc.), and frequency values in Hz (e.g., 466/440, 660,440, 880/440, etc.) may also be entered. All values are rounded to 3 decimal places. For example, enter the just (5-limit) perfect fifth 3/2 and the program will report its decimal equivalent as 1.5 and its size in cents as 701.955 cents. For more information, see my ATMI 2012 presentation.

Current version: 2.04

Released: 6/25/21

Used in the following course: MUSC 726T Tuning Theory

Reference: Gann 2019

Download SLAPI for Mac (.dmg) Download SLAPI for Windows (.zip)

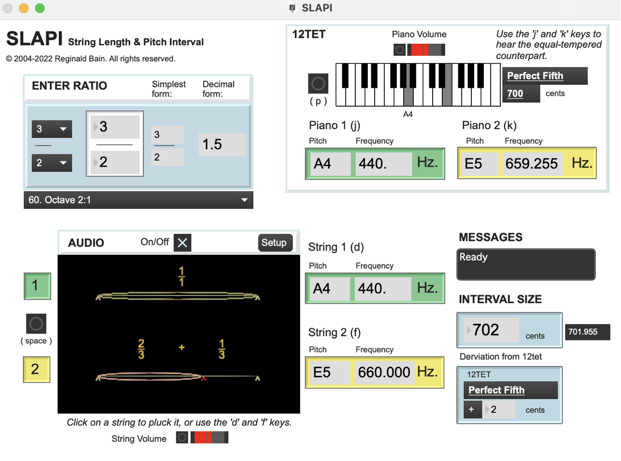
SLAPI: A harmonic series interval player for Mac OS and Windows

SLAPI, or String Length and Pitch Interval, is a harmonic series interval player. It provides students with an easy way to compare the size of pitch intervals represented as frequency ratios with their equal-tempered counterparts. For example if the student enters the ratio 3/2, SLAPI will calculate the frequency above A4 that corresponds with that ratio (660 Hz) and allow the student to interactively play the interval's component pitches using a sampled Karplus-Strong plucked string tone. The program also creates two proportional string length division diagrams for the frequency ration, and reports it the frequency ratio's decimal equivalent (1.5), size in cents (702 cents), and deviation from equal temperament (+2 cents). The equal-tempered counterpart's pitches (A4–E5; 440–659.255 Hz) are played used a piano sample and may be superimposed over the string tones so that beating patterns may be perceived.

Current version: v2.0

Released: 9/7/22

System Requirements: SLAPI is a standalone application built with Max 8. For system requirements, see Cycling '74, Max 8 System Requirments

Documentation: pdf (coming soon)

Used in the following courses:

1. MUSC 215 Music Theory III
2. MUSC 726T Tuning Theory

References: Gann 2019; Campbell & Greated 2001

References

Campbell, Murray and Clive Greated. 2001/1987. The Musician's Guide to Acoustics. New York: Oxford University Press.

Gann, Kyle. 2019. The Arithmetic of Listening: Tuning Theory and History for the Impractical Musician. Urbana, IL: University of Illinois Press.

Morris, Robert. 1987. Composition with Pitch Classes. New Haven: Yale University Press.

Rahn, John. 1980. Basic Atonal Theory. New York: Longman.

Straus, Joseph N. 2016. Introduction to Post-Tonal Theory, 4th ed. New York: Norton.

Toussaint, Godfried T. 2013. The Geometry of Musical Rhythm: What Makes a "Good" Rhythm Good?, 1st ed. Boca Raton, FL: CRC Press.

Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press.